"Wiedza i Życie"
Zjawisko Mössbauera jest związane z emisją i absorpcją promieniowania γ przez jądra atomowe. Przypomnijmy najpierw jak absorpcja i emisja rezonansowa wygląda w przypadku atomów. Jeżeli skierujemy na dany atom znajdujący się w stanie podstawowym promieniowanie o energii równej energii przejścia do stanu wzbudzonego, to atom ten pochłonie kwant promieniowania przechodząc jednocześnie do stanu wzbudzonego. Po określonym czasie (czas życia poziomu wzbudzonego) następuje deekscytacja do stanu podstawowego - atom emituje kwant promieniowania o częstości równej (z dobrym przybliżeniem) częstości kwantu pochłoniętego.
Podobna sytuacja powinna mieć miejsce w przypadku wzbudzania poziomów jądrowych. Jednak tutaj absorpcja rezonansowa w tak prosty sposób na ogół nie da się zrealizować, a to ze względu na znaczną wartość energii odrzutu towarzyszącej emisji i absorpcji promieniowania z jądra atomowego. Aby wykazać różnice między procesami rezonansowymi zachodzącymi w atomie i jądrze należy zwrócić uwagę na dwa czynniki:
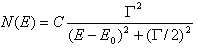
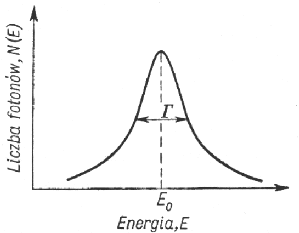
Γ - szerokość połówkowa krzywej,
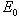 - energia fotonu, dla którego prawdopodobieństwo emisji jest największe,
- energia fotonu, dla którego prawdopodobieństwo emisji jest największe,
C - stała.
Aby oszacować naturalną szerokość połówkową poziomu jądrowego czy atomowego wystarczy skorzystać wprost z zasady nieoznaczoności dla energii i czasu: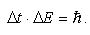
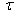 a odchylenie energetyczne ΔE zastąpimy szerokością połówkową poziomu Γ to otrzymamy relację:
a odchylenie energetyczne ΔE zastąpimy szerokością połówkową poziomu Γ to otrzymamy relację:
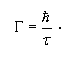
Typowe czasy życia atomowych stanów wzbudzonych mają wartości rzędu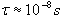 co daje szerokość naturalną poziomu około
co daje szerokość naturalną poziomu około 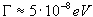 .
Natomiast czasy życia jądrowych poziomów wzbudzonych są zdecydowanie krótsze,
.
Natomiast czasy życia jądrowych poziomów wzbudzonych są zdecydowanie krótsze, 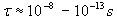 , co skutkuje większą szerokością naturalną wzbudzonego poziomu jądrowego:
, co skutkuje większą szerokością naturalną wzbudzonego poziomu jądrowego: 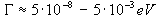 .
.
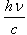 :
:
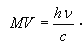
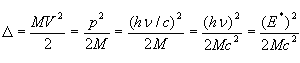
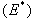 - energia wzbudzenia,
- energia wzbudzenia,
M - masa (atomu w przypadku przejść atomowych lub jądra w przypadku przejść jądrowych),
c - prędkość światła. Analizując wyrażenie na energię odrzutu: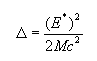
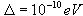 i jest o dwa rzędy wielkości niższa od naturalnej szerokości poziomu.
Stąd też procesy rezonansowe w atomie są łatwe do zauważenia.
W przypadku przejść jądrowych, energia odrzutu jądra swobodnego przyjmuje
wartości z zakresu
i jest o dwa rzędy wielkości niższa od naturalnej szerokości poziomu.
Stąd też procesy rezonansowe w atomie są łatwe do zauważenia.
W przypadku przejść jądrowych, energia odrzutu jądra swobodnego przyjmuje
wartości z zakresu 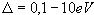 i o kilka rzędów wielkości przekracza naturalną szerokość poziomu jądrowego.
Stąd też teoretycznie rezonansowa absorpcja jądra swobodnego jest niemożliwa do przeprowadzenia.
i o kilka rzędów wielkości przekracza naturalną szerokość poziomu jądrowego.
Stąd też teoretycznie rezonansowa absorpcja jądra swobodnego jest niemożliwa do przeprowadzenia.
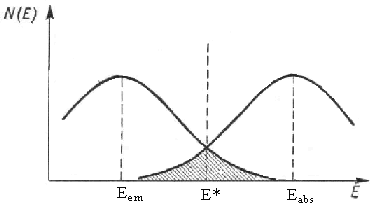
Zauważmy, że podczas emisji promieniowania jądrowego kwant γ unosi energię pomniejszoną o energię odrzutu jądra Δ. Natomiast odwrotnie wygląda sytuacja w przypadku absorpcji, kiedy to kwant γ musi mieć energię na tyle dużą, aby skompensowała nie tylko energię wzbudzenia ale również energię odrzutu. Dlatego też linie emisyjna i absorpcyjna w skali energii będą przesunięte względem siebie o wartość 2Δ.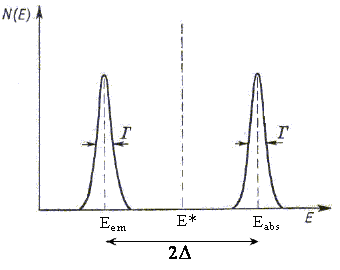
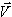 tak, że wektor prędkości tworzy z kierunkiem emisji fotonu kąt φ:
tak, że wektor prędkości tworzy z kierunkiem emisji fotonu kąt φ:
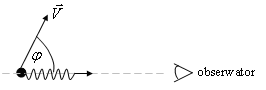
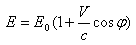
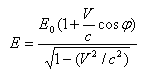
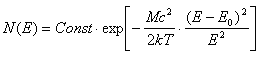
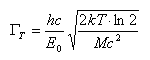
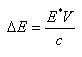
Zjawisko to najprościej jest objaśnić w oparciu o model Einsteina drgań sieci krystalicznej, który traktuje N-atomową próbkę krystaliczną jako zbiór 3N oscylatorów harmonicznych mających tę sama częstość drgań ω. Stan kryształu określany jest natomiast przez liczby kwantowe oscylatorów. Przejmowanie pędu odrzutu przez cały kryształ wynika z tego, że sieć krystaliczna nie może przyjąć dowolnej wartości energii. Zmiana stanu drgań sieci może odbyć się tylko przez emisję lub absorpcję fononów o energii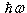 ,
która zazwyczaj ma wartość rzędu 10-2eV. Tak, więc sieć krystaliczna w procesie emisji lub absorpcji fotonu może
przyjąć tylko porcje energii będące całkowitymi wielokrotnościami
,
która zazwyczaj ma wartość rzędu 10-2eV. Tak, więc sieć krystaliczna w procesie emisji lub absorpcji fotonu może
przyjąć tylko porcje energii będące całkowitymi wielokrotnościami 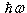 , czemu towarzyszy kreacja odpowiedniej liczby
fononów. Żeby zrozumieć kiedy ma szanse zajść proces rozpraszania rezonansowego należy rozpatrzeć trzy przypadki:
, czemu towarzyszy kreacja odpowiedniej liczby
fononów. Żeby zrozumieć kiedy ma szanse zajść proces rozpraszania rezonansowego należy rozpatrzeć trzy przypadki:
Skomentuj tekst
Podobna sytuacja powinna mieć miejsce w przypadku wzbudzania poziomów jądrowych. Jednak tutaj absorpcja rezonansowa w tak prosty sposób na ogół nie da się zrealizować, a to ze względu na znaczną wartość energii odrzutu towarzyszącej emisji i absorpcji promieniowania z jądra atomowego. Aby wykazać różnice między procesami rezonansowymi zachodzącymi w atomie i jądrze należy zwrócić uwagę na dwa czynniki:
- szerokość naturalną energetycznego poziomu jądrowego i atomowego,
- wartość energii odrzutu w przypadku emisji atomowej i jądrowej a także wartość energii promieniowania atomowego i jądrowego.
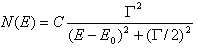
Γ - szerokość połówkowa krzywej,
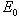 - energia fotonu, dla którego prawdopodobieństwo emisji jest największe,
- energia fotonu, dla którego prawdopodobieństwo emisji jest największe,C - stała.

Aby oszacować naturalną szerokość połówkową poziomu jądrowego czy atomowego wystarczy skorzystać wprost z zasady nieoznaczoności dla energii i czasu:
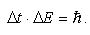
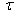 a odchylenie energetyczne ΔE zastąpimy szerokością połówkową poziomu Γ to otrzymamy relację:
a odchylenie energetyczne ΔE zastąpimy szerokością połówkową poziomu Γ to otrzymamy relację:
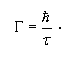
Typowe czasy życia atomowych stanów wzbudzonych mają wartości rzędu
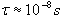 co daje szerokość naturalną poziomu około
co daje szerokość naturalną poziomu około 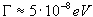 .
Natomiast czasy życia jądrowych poziomów wzbudzonych są zdecydowanie krótsze,
.
Natomiast czasy życia jądrowych poziomów wzbudzonych są zdecydowanie krótsze, 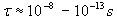 , co skutkuje większą szerokością naturalną wzbudzonego poziomu jądrowego:
, co skutkuje większą szerokością naturalną wzbudzonego poziomu jądrowego: 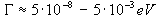 .
.
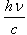 :
:
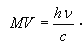
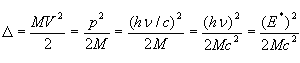
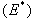 - energia wzbudzenia,
- energia wzbudzenia,M - masa (atomu w przypadku przejść atomowych lub jądra w przypadku przejść jądrowych),
c - prędkość światła. Analizując wyrażenie na energię odrzutu:
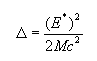
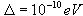 i jest o dwa rzędy wielkości niższa od naturalnej szerokości poziomu.
Stąd też procesy rezonansowe w atomie są łatwe do zauważenia.
W przypadku przejść jądrowych, energia odrzutu jądra swobodnego przyjmuje
wartości z zakresu
i jest o dwa rzędy wielkości niższa od naturalnej szerokości poziomu.
Stąd też procesy rezonansowe w atomie są łatwe do zauważenia.
W przypadku przejść jądrowych, energia odrzutu jądra swobodnego przyjmuje
wartości z zakresu 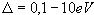 i o kilka rzędów wielkości przekracza naturalną szerokość poziomu jądrowego.
Stąd też teoretycznie rezonansowa absorpcja jądra swobodnego jest niemożliwa do przeprowadzenia.
i o kilka rzędów wielkości przekracza naturalną szerokość poziomu jądrowego.
Stąd też teoretycznie rezonansowa absorpcja jądra swobodnego jest niemożliwa do przeprowadzenia. Zauważmy, że podczas emisji promieniowania jądrowego kwant γ unosi energię pomniejszoną o energię odrzutu jądra Δ. Natomiast odwrotnie wygląda sytuacja w przypadku absorpcji, kiedy to kwant γ musi mieć energię na tyle dużą, aby skompensowała nie tylko energię wzbudzenia ale również energię odrzutu. Dlatego też linie emisyjna i absorpcyjna w skali energii będą przesunięte względem siebie o wartość 2Δ.

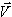 tak, że wektor prędkości tworzy z kierunkiem emisji fotonu kąt φ:
tak, że wektor prędkości tworzy z kierunkiem emisji fotonu kąt φ:
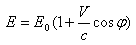
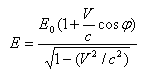
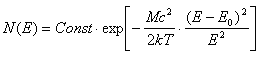
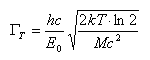

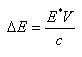
Zjawisko to najprościej jest objaśnić w oparciu o model Einsteina drgań sieci krystalicznej, który traktuje N-atomową próbkę krystaliczną jako zbiór 3N oscylatorów harmonicznych mających tę sama częstość drgań ω. Stan kryształu określany jest natomiast przez liczby kwantowe oscylatorów. Przejmowanie pędu odrzutu przez cały kryształ wynika z tego, że sieć krystaliczna nie może przyjąć dowolnej wartości energii. Zmiana stanu drgań sieci może odbyć się tylko przez emisję lub absorpcję fononów o energii
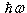 ,
która zazwyczaj ma wartość rzędu 10-2eV. Tak, więc sieć krystaliczna w procesie emisji lub absorpcji fotonu może
przyjąć tylko porcje energii będące całkowitymi wielokrotnościami
,
która zazwyczaj ma wartość rzędu 10-2eV. Tak, więc sieć krystaliczna w procesie emisji lub absorpcji fotonu może
przyjąć tylko porcje energii będące całkowitymi wielokrotnościami 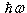 , czemu towarzyszy kreacja odpowiedniej liczby
fononów. Żeby zrozumieć kiedy ma szanse zajść proces rozpraszania rezonansowego należy rozpatrzeć trzy przypadki:
, czemu towarzyszy kreacja odpowiedniej liczby
fononów. Żeby zrozumieć kiedy ma szanse zajść proces rozpraszania rezonansowego należy rozpatrzeć trzy przypadki:
- Jeżeli energia odrzutu jest większa od energii wiązania atomu w krysztale (10-30 eV) to na skutek procesu emisji kwantu γ atom zostanie wyrzucony ze swego położenia w sieci a cały proces emisji można opisywać tak jak dla atomu swobodnego.
- Jeżeli energia odrzutu jest większa od charakterystycznej energii drgań sieci (energii fononu), ale mniejsza od energii wiązania atomu w krysztale to atom nie zostaje wybity ze swego położenia w sieci a energia odrzutu zostaje zużyta na pobudzenie drgań sieci (kreację określonej liczby fononów).
- Jeżeli energia odrzutu jest mniejsza od energii fononu sieć nie zostanie wzbudzona a pęd odrzutu przejmie kryształ jako całość. Taki proces nazywamy bezfononowym, lub inaczej emisją bezodrzutową a od nazwiska odkrywcy został nazwany też efektem Mössbauera.
20.04.2007 T.Pikula
Opracowano na podstawie:
1. G. Wertheim, Mössbauer Effect: Principles and Applications, Academic Press, New York (1964).
2. T. Goworek, Zjawisko Mössbauera, w tomie "Metody doświadczalne w fizyce ciała stałego", redaktor M. Subotowicz, UMCS, Lublin 1976, s.312.
3. A. Hrynkiewicz, "Efekt Mössbauera i jego zastosowanie w fizyce ciała stałego" w tomie "Cząstki elementarne, jądro atomowe, promieniotwórczość" PWN, Warszawa, 1976.
1. G. Wertheim, Mössbauer Effect: Principles and Applications, Academic Press, New York (1964).
2. T. Goworek, Zjawisko Mössbauera, w tomie "Metody doświadczalne w fizyce ciała stałego", redaktor M. Subotowicz, UMCS, Lublin 1976, s.312.
3. A. Hrynkiewicz, "Efekt Mössbauera i jego zastosowanie w fizyce ciała stałego" w tomie "Cząstki elementarne, jądro atomowe, promieniotwórczość" PWN, Warszawa, 1976.